Rufen Sie uns einfach an, und wir beraten Sie gerne zu unserem Seminar- und Studienangebot.
Unsere Ansprechpartner:

Michael Rabbat, Dipl.-Kfm.
MBA Chief Operating Officer

Claudia Hardmeier
Kunden-Center
Studienbetreuung
2.6.2 Dynamic methods
Major difference to the static methods of capital budgeting is that dynamic methods consider the time value of money. In consequence the project’s cash flows over the project life time are discounted to today’s of money.
Today’s value of money differs from the value in the future because if invested it would earn interest over time.
The present value of an amount of cash at some future date is calculated8
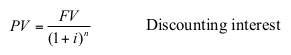
With FV= future value, PV = present value, i = discounting factor (interest rate or cost of capital), n = number of periods
The NPV method
The net present value (NPV) represents the sum of the present value of future cash flows discounted to today at a given intereset rate.
NPV compares the present value of money today to the present value of money in the future.
![]()
calculating the net present value
With FV= future value, PV = present value, i = the rate of return; the opportunity cost of capital, N = number of periods, I0 = initial investment
The rate of return used to discount future cash flows is either the cost of capital9 or the rate of return of an investment with similar risk, also called opportunity cost10.
If the NPV is positive the investment is creating more value than alternative investments with the applied rate of return.
The IRR method
The internal rate of return (IRR) is defined as the rate of return (interest) that makes the net present value equal to zero.
![]()
With FV= future value, PV = present value, IRR = internal rate of return, N = number of periods, I0 = initial investment
If the IRR is greater than the cost of capital, the project is creating value. The IRR method provides relative values for the return compared with the absolute results of the NPV method. The IRR is interpreted according to Volckart as a rate of return per period for the capital still tied-up during that period11. Other interpretations assume reinvestment of interim cash flows in projects with equal rates of return (the reinvestment can be the same project or a different project). Therefore, IRR overstates the annual equivalent rate of return for a project whose interim cash flows are reinvested at a rate lower than the calculated IRR12.
For this reason the IRR should not be used to rate mutually exclusive projects, but only to decide whether a single project is worth investing in.
NPV vs IRR
Applying the method of NPV or IRR for the same project gives usually the same answer to the question if the investment creates value or not.
In case different projects (different in initial investment, life time, pay back characteristics) are compared and rated, the question which investment adds more value is not answered equally, but depending on the applied method of calculation. The rating of the rate of return for different projects requires more detailed evaluation13 and is not discussed in this paper.
Choosing the appropriate method for capital budgeting
Given the character of an IP (long life time, dynamic income, and dynamic expenditure), dynamic methods are the preferred techniques to calculate the IP’s economic value even if they require more time and effort for data collection and calculation compared to static capital budgeting methods. The advantages of dynamic methods as the consideration of the time value of money and the effective cash flows instead of average values enable a more detailed analysis of the investment project and, given the investment volume and the project’s life-time, are therefore of advantage.
The required input data for the capital budgeting are based on the results of the studies prepared during the pre-investment phase14.
| Result | Source |
|---|---|
| The required investments until project completion are known with certain accuracy. The more detailed the studies the better the accuracy of the investments estimate. | Scope definition |
| The time schedule for the investment phase and the corresponding cash requirement plan has been drawn | Time scheduling
Cash flow schedule |
| The expected revenues from the sale of product are forecasted. | Market studies |
| Costs of operation are estimated over the lifetime of the project | Technology selection and feedstock price |
Table 4: Input data for capital budgeting
Calculating the project’s periodic cash flows
The cash flows of every period during the project’s lifetime are calculated according to common practise15 and discounted to the present value and evaluated with different methods of capital budgeting.
| Net revenues | Example |
|---|---|
| / Cost of operation | Cost for feedstock, raw materials, consumables, salaries, etc |
| / Depreciation | According to applicable tax law |
| / Overhead cost | Administrative cost, insurance premiums, land rent |
| EBIT | |
| / Interest | Payable to lenders |
| / Tax | According to applicable tax law |
| Net earnings | |
| + Depreciation | According to applicable tax law |
| / ∆ Reserves | Change in provisions, accruals |
| / ∆ Net working capital | Change in storage, receivables, cash |
| Operating cash flow | |
| / Reinvestment | Replacement of existing facilities |
| / Loan payback | Payable to lenders |
| Free cash flow | |
| + interest | |
| Cash flow to calculate NPV and IRR | |
Table 5: Calculation of project cash flow
8 Volckart p 186, 187
9 Investitionsrechnung, WRW Verlag, 3. Auflage 2010, p 20
10 Wikipedia.org „Net present value”, Jan 3rd, 2013
11 Volckart p 287, 293
12 Investitionsrechnung, WRW Verlag, 3. Auflage 2010, p 27ff
13 Volckart p 285, Investitionsrechnung, WRW Verlag, 3. Auflage 2010, p 30ff
14 See chapter 4.2
15 according to Volckart page 591







