5.2. Lineare Optimierung

Eine der bekanntesten und meist eingesetzten OR-Methoden ist die Lineare Optimierung. „Unter Linearer Optimierung versteht man die Optimierung, d.h. Maximierung oder Minimierung einer linearen Funktion, der sogenannten Zielfunktion, deren Variablen einem System von Ungleichungen, den sogenannten Restriktionen genügen müssen.“¹²¹ Typische Einsatzfelder der Linearen Optimierung sind:

• Die Planung von Produktionsprogrammen mit dem Ziel der Kostenminimierung oder Gewinnmaximierung unter Einhaltung von Kapazitäts oder sonstigen Beschränkungen.
• Die Optimierung von Mischungsverhältnissen mit dem Ziel der Kostenminimierung unter Einhaltung bestimmter Eigenschaften der Mischung.
• Die Planung von Zuschnitten mit dem Ziel einer Reduktion des Materialabfalls.¹²²

Zielfunktion und Restriktionen (auch Nebenbedingungen) entsprechen linearen Gleichungen bzw. Ungleichungen. Hieraus stammt die Bezeichnung Lineares Optimierungsproblem. Ein Spezialfall ist das Standardmaximalproblem, bei dem der Zielfunktionswert maximiert werden soll und die Nebenbedingungen obere Schranken bilden. Es hat die Struktur:¹²³

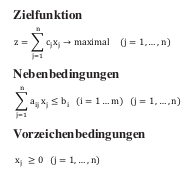
Erläuterung der Variablen

z: zu maximierender Zielfunktionswert [z. B. gesamter Deckungsbeitrag eines Produktionsprogramms]

xj: Entscheidungsvariablen [z. B. Anzahl zu produzierender Produkte je Produktvariante j]

cj: Zielbeitrag [z. B. Deckungsbeitrag eines Produktes der Produktvariante j]

n: Anzahl der Entscheidungen [z. B. Anzahl aller Produktvarianten]

bi: Ressourcen-Fonds [z. B. zur Verfügung stehende Produktionskapazität je Maschine i]

aij: Ressourcenverbrauch [z. B. Kapazitätsbedarf je Produkt der Produktvariante j auf der Maschine i]

m: Anzahl Ressourcen [z. B. Anzahl verschiedener Maschinen im Produktionsprozess]

j/i: Indizes [j: Produktvariante, i: Maschine]

Formel 1: Standardmaximalproblem / Lineares Optimierungsproblem

Mit der Simplex-Methode entwickelte G. B. Danzig 1947 eines der bedeutendsten Verfahren zur Lösung Linearer Optimierungsprobleme. Es basiert auf einem Algorithmus, führt immer zur optimalen Lösung (sofern das Gleichungssystem lösbar ist) und lässt sich auch manuell berechnen. Bei einer hohen Anzahl an Nebenbedingungen und Entscheidungsvariablen des Gleichungssystems ist jedoch nur eine EDV-gestützte Lösung praktikabel.¹²⁴ Neben Spezialsoftware steht hierfür aktuell vor allem eine in Microsoft Excel integrierte und somit weit verbreitete Berechnungsroutine (Solver) zur Verfügung.¹²⁵,¹²⁶

Ein weiterer Spezialfall tritt ein, wenn die Lösungsmenge nur Ganze Zahlen beinhalten darf. Ganzzahlige Lösungen kommen bei praktischen Fragestellungen häufig vor. So können z. B. bei der Optimierung von Investitionsprogrammen nur ganze Maschinen eingesetzt werden und bei der Produktionsplanung nur ganze Produkte erzeugt werden. Im mathematischen Modell äußert sich dies durch die zusätzliche Bedingung, dass alle Entscheidungsvariablen (xj) ganzzahlig sein müssen.¹²⁷

Die Forderung nach Ganzzahligkeit führt nicht zu einer Vereinfachung des Modells. Sie erhöht, insbesondere bei Problemen mit einer größeren Anzahl an Variablen und Nebenbedingungen, den Rechenaufwand erheblich. Hinzu kommt, dass der Zielfunktionswert (z) im Fall eines ganzzahligen Optimierungsproblems meist schlechter wird, als bei einem vergleichbaren Problem ohne den Anspruch an Ganzzahligkeit.¹²⁸,¹²⁹ Verfahren zur Lösung von ganzzahligen Optimierungsproblemen sind das Graphische Verfahren, das Schnittebenen-Verfahren, das Entscheidungsbaum-Verfahren und Heuristische Verfahren.¹³⁰ Auf ihre vertiefende Erläuterung wird verzichtet, da zur Berechnung der Microsoft Excel-Solver eingesetzt wird.

In der praktischen Anwendung bestehen ganzzahlige Optimierungsprobleme auch in der Form, dass die Lösung ihrer Entscheidungsvariablen (xj) auf die Werte 0 und 1 beschränkt ist. In solchen Fällen ist die Rede von 0-1-Problemen oder auch Boole ́schen Problemen.¹³¹ Diese Ausprägung des Optimierungsproblems besitzt hohe Relevanz, da sich damit Entscheidungen gut abbilden lassen, die eine logische Struktur (ja/nein) aufweisen. Beispiele hierfür sind die Durchführung von Investitionen innerhalb eines Investitionsprogrammes aber auch die Aufnahme von Projekten in ein Projektportfolio.

¹²¹ Zimmermann W. / Stache U. (Operations Research), S.48
¹²² Vgl. Zimmermann W. / Stache U. (Operations Research), S.48
¹²³ Vgl. Stingl P. (Operations), S.3ff. und S.20
¹²⁴ Vgl. Zimmermann W. / Stache U. (Operations Research), S.5
¹²⁵ Vgl. Zimmermann J. / Stark C. / Rieck J. (Projektplanung), S.33
¹²⁶ Siehe Anhang 11: Einstellung des Microsoft Excel-Solvers; Microsoft Excel ist eine eingetragene Marke der Microsoft Corporation. Der Einsatz setzt den Erwerb einer entsprechenden Produktlizenz voraus.
¹²⁷ Vgl. Zimmermann W. / Stache U. (Operations Research), S.125
¹²⁸ Der Zielfunktionswert des ganzzahligen Optimierungsproblems kann bestenfalls den Wert des Standardmaximalproblems annehmen, ihn aber nicht übersteigen.
¹²⁹ Vgl. Stingl P. (Operations), S.104f.
¹³⁰ Vgl. Zimmermann W. / Stache U. (Operations Research), S.125
¹³¹ Vgl. Zimmermann W. / Stache U. (Operations Research), S.125