5.4. Anwendungsbeispiel

Ausgangspunkt des Beispiels ist der im Kapitel 4.3 Planungsprozess zum Projektportfolio dargestellte Umsetzungsvorschlag mit seinem Ressourcenbedarf. Die Auswahl basiert auf einem vorab durchgeführten Projektscoring in Form einer Nutzwertanalyse und daraus abgeleiteten Projektprioritäten. Angenommen wird ein unternehmensweites Projektbudget in Höhe von 700 TEUR und Mitarbeiterressourcen für Projekte von maximal 35,00 Vollbeschäftigungseinheiten (VbE).

Bei Umsetzung der Empfehlung des MPM käme es zur Durchführung eines Projektportfolios, dessen Wertschöpfung (ausgedrückt als kumulierter Projektscore ohne Beachtung der Zwangsprojekte) 21,13 Punkte betragen würde. Das Portfolio würde zu Budgetanforderungen in Höhe von 580 TEUR führen und Mitarbeiterkapazitäten in Höhe von 34,44 VbE benötigen:

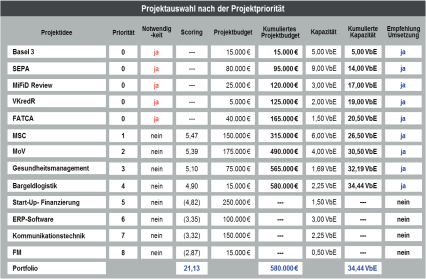
Abb. 5: Ursprüngliches Ergebnis der Projektauswahl nach Projektpriorität¹³⁴

Die analogen Daten zu den Projekten und Ressourcen werden nun im mathematischen Modell (siehe Kapitel 5.3) erfasst. Wie bei einer Auswahl der Projekte nach ihrer Priorität werden Zwangsprojekte aus der Selektion ausgeklammert, d.h. ihre Umsetzung erfolgt unbeschadet der Berechnungsergebnisse. Es verbleiben 8 potenzielle Projekte, welche bei vollständiger Umsetzung einen maximalen Portfoliowert in Höhe von 35,49 Punkten erziele könnten. Gesucht wird diejenige Projektkombination, die diesem Wert am nächsten kommt:

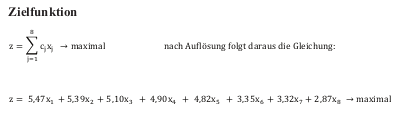
Es können jedoch nicht alle Projekte durchgeführt werden, da das gesamte Budget und die vorhandenen Kapazitäten begrenzt sind. Die Ressourcenanforderungen der Zwangsprojekte mindern zudem die zur Verfügung stehenden Fonds. Nach Abzug der somit schon zugewiesenen Ressourcen verbleiben:

• ein Budget in Höhe von 535 TEUR (700 TEUR – 165 TEUR) und
• Projektkapazitäten in Höhe von 14,50 VbE (35,00 VbE - 20,50 VbE).

Diese Ressourcen würden bei vollständiger Umsetzung aller Projektalternativen mit 965 TEUR Budget und 21,44 VbE deutlich überschritten. Die gesuchte Projektkombination muss damit innerhalb der Restriktionen bleiben:

Es wird für alle 8 Projekte geprüft, ob sie in das Portfolio aufzunehmen sind. Dies wird Zuweisung der Werte 1 oder 0 zu jeweiligen Entscheidungsvariablen (x_j) ausgedrückt:

Lösungsmenge

x_j ∈ {0,1}

Formel 3: Beispiel zur Linearen Optimierung bei der Projektauswahl

Die Berechnung erfolgt mit Hilfe des Microsoft Excel-Solvers.¹³⁵,¹³⁶

Im Ergebnis resultiert ein Portfolio, dessen Wertschöpfung mit 24,93 Punkten um 3,80 Punkte höher ist als beim ursprünglichen Vorgehen nach Projektpriorität. Die Budget- und Kapazitätsvorgaben werden mit 695 TEUR und 34,19 VbE (530 TEUR und 13,69 VbE ohne Zwangsprojekte) eingehalten. Überraschender Weise wird gerade das Projekt mit dem höchsten Projektscore nicht zur Umsetzung empfohlen. Stattdessen sollen die 3 letzten Projekte der Rangliste realisiert werden. Im Vorschlag steigt das Portfoliobudget um 115 TEUR. Es bleibt aber innerhalb der Restriktion. Der Kapazitätsbedarf sinkt hingegen leicht:

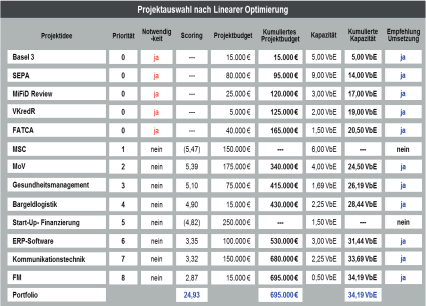
Abb. 6: Ergebnis der Projektauswahl nach Linearer Optimierung¹³⁷

Das Optimierungsmodell wird im folgenden Kapitel bewertet und hinsichtlich seiner Aussagekraft und Einsatzmöglichkeiten analysiert.

¹³⁴ Eigene Darstellung
¹³⁵ Siehe Anhang 12: Projektauswahl nach Anwendung des Excel-Solvers
¹³⁶ Da es theoretisch, vor allem bei umfangreicheren Portfolios, auch mehrere optimale Projektkombinationen geben kann, empfiehlt es sich, die Bearbeitungsroutine der Software mehrfach anzustoßen, um solche Sonderfälle zu identifizieren. Die Auswahl erfolgt dann ggf. an Hand des geringsten Ressourcenbedarfs.
¹³⁷ Eigene Darstellung