5.3. Übertragung auf die Projektportfolioplanung

Wie im Verlauf dieser Arbeit bereits dargestellt, hat die Unternehmensleitung im Rahmen der PPP Entscheidungen zu treffen, welche Projekte aus einer Menge möglicher Projektideen in der jeweiligen Planungsperiode durchzuführen sind, d. h. in das Projektportfolio aufgenommen werden sollen. Angenommen wird dazu eine Gesamtmenge (n) an Projekten, bei denen der Index (j) das jeweilige Projekt kennzeichnet. Die Entscheidungsvariablen (xj) können die Werte 0 oder 1 annehmen. Erhält eine Entscheidungsvariable im Ergebnis der Berechnung den Wert 1, wird das jeweilige Projekt ins Portfolio aufgenommen. Erhält sie hingegen den Wert 0 wird das Projekt nicht durchgeführt.

Der Zielfunktionswert (z) entspricht der gesamten Wertschöpfung des Projektport folios als Teilmenge aller möglichen Projekte und wird maximiert. Er ergibt sich als Summe der Einzelnutzen (cj) aller durchzuführenden Projekte. Der Nutzen der Projekte muss als Projektscore einheitlich quantifizert vorliegen.

Für die Durchführung des Projektportfolios wird eine Anzahl (m) an Ressourcen benötigt. Die jeweiligen Ressourcen werden mid dem Index (i) gekennzeichnet. Für die Durchführung von Projekt (j) werden (aij) Einheiten der Ressource (i) benötigt. Von Ressource (i) stehen im Planungszeitraum insgesamt nur (bi) Einheiten bereit. Typische auf eine Planungsperiode bezogene Ressourcenbeschränkungen für Projekte bestehen in Budgetvorgaben oder Kapazitäten-Fonds für die Projektmitarbeiter.¹³²

Aus diesen Angaben wird ein Lineares Optimierungsproblem aufgestellt:¹³³

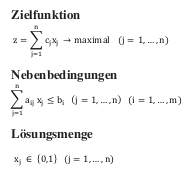
Erläuterung der der Variablen

z: Zielfunktionswert [gesamte Wertschöpfung des Projektportfolios, z. B. Summe der Projektscores]

xj: Entscheidungsvariablen [Durchführung des Projektes j: nein/ja]

cj: Zielbeitrag [Nutzen des Projektes j, z. B. Projektscore]

n: Anzahl zu treffender Entscheidungen [Anzahl mögliche Projekte]

bi: Ressourcen-Fonds [von Ressource i insgesamt zur Verfügung stehende Einheiten]

aij: Ressourcenverbrauch [Inanspruchnahme der Ressource i durch das Projekt j]

m: Anzahl Ressourcen [Anzahl verschiedener einzuhaltender Ressourcen]

j/i: Indizes [j: Projekte, i: Ressourcen]

Formel 2: Lineares Optimierungsmodell zur Projektauswahl

Das so erstellte mathematische Modell zur Unterstützung der Projektselektion im Rahmen der PPP wird nachfolgend an Hand eines Beispiels illustriert.

¹³² Vgl. Zimmermann J. / Stark C. / Rieck J. (Projektplanung), S.32f.
¹³³ Vgl. Zimmermann J. / Stark C. / Rieck J. (Projektplanung), S.33