2.2.4.1.1 Value-at-Risk-Modell / Earnings-at-Risk-Modell

Zu den mathematisch-statistischen Bewertungsverfahren, die sich in den letzten Jahren als „Marktstandard“ durchgesetzt haben und auch von der aufsichtrechtlichen Behörde (BaFin) unterstützt werden, gehören das Value-at-Risk-Konzept (VaR) oder auch das Earnings-at-Risk-Konzept (EaR). Bei diesen Konzepten steht das Ziel im Vordergrund, eine Risikomessgröße zu erhalten, die möglichst universell einsetzbar und gut inter-pretierbar ist sowie einen Vergleich mit von eintretenden Risiken betroffenen Ergebnis- oder auch Kapitalgrößen erlaubt. Im Zuge der Erweiterung des ganzheitlichen inte-grierten Risikomanagements rückte zunehmend der EaR-Ansatz für Bewertung der Geschäftsrisiken in den Fokus.

Das Risiko resultiert normalerweise aus der Veränderung der (Markt)verhältnisse, die nicht von vornherein erkannt, aber als Zufallsvariable aufgefasst werden können. Durch ein geeignetes Verfahren können eine Wahrscheinlichkeitsverteilung und ein Quantil¹²⁴ bestimmt werden. Daraus ergibt sich, welchen Wert die Zufallsvariable mit einer gewissen Wahrscheinlichkeit nicht überschreitet. Dieser Wert wird durch den VaR dargestellt.

Damit stellt der VaR die geschätzte mit einer vorgegebenen Wahrscheinlichkeit (Konfidenzniveau) und einer bestimmten Verteilungsannahme (z.B. der Normalverteilung) innerhalb einer bestimmten Periode (Haltedauer) nicht überschrittene maximale negative Wertänderung (Verlust) einer Position dar.¹²⁵

Grundsätzlich kann die Quantifizierung des im Rahmen dieser Arbeit zu betrachtenden EaR, auf zwei Wegen erfolgen, analytisch oder durch Simulation. Zunächst wird die analytische Vorgehensweise betrachtet, die gemäß Schierenbeck/Lister durch ein mehrstufiges Verfahren¹²⁶ gekennzeichnet ist und die prägenden Kernbausteine Verteilungsart, Sicherheitsniveau, Risikoperiode und Datenbasis berücksichtigt.¹²⁷

Im ersten Schritt werden die relevanten Risikoparameter definiert. In der einfachsten Betrachtungsebene können dies für die EaR die Parameter geschäftsrisikorelevanter Ertrag und geschäftsrisikorelevante Kosten sein.

Im zweiten Schritt folgt die Ermittlung der Volatilität des jeweiligen Risikoparameters. Auf Basis eine Reihe historischer Daten wird der Mittelwert berechnet. Unter der Annahme, dass sich die Daten der Zukunft entsprechend der Ergebnisse der Vergangenheit verhalten, kann der Mittelwert dem zukünftigen Erwartungswert gleichgesetzt werden.

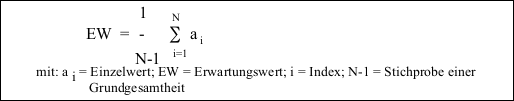
Der Erwartungswert bildet die Grundlage der Berechnung der Varianz, aus deren Quadratwurzel die Standardabweichung folgt:

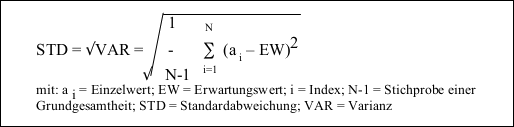
Aus verteilungstheoretischer Sicht ist zudem zur Verbesserung der Ergebnisgenauigkeit mit logarithmierten Werten zu rechnen.

Der Erwartungswert und die Standardabeichung bilden die Basis für die Festlegung der Häufigkeits- bzw. Wahrscheinlichkeitsverteilung. Auf Basis dieser Verteilungen können Aussagen getroffen werden, wie hoch der bei einem bestimmten vorzugebenden Wahrscheinlichkeitsniveau maximal auftretende Verlust ausfallen kann. Dabei lässt sich aus der sogenannten Dichtefunktion einer Verteilung ablesen, mit welcher Wahrscheinlichkeit ein bestimmter Wert beobachtet werden konnte. Die Fläche unterhalb dieser Dichtefunktion entspricht demnach 100% aller Fälle. Zur Vereinfachung wird häufig versucht, die jeweiligen Wahrscheinlichkeitsverteilungen auf standardisierte idealtypische Verteilungsformen zurückzuführen. In den Veröffentlichungen der deutschen Kreditinstitute wird für das Geschäftsrisiko durchgängig die Standard-Normalverteilung analog dem Marktpreisrisiko unterstellt.

Eine weitere entscheidende Größe des EaR-Konzeptes ist das Sicherheits- bzw. Konfidenzniveau 1-α, d.h. die Wahrscheinlichkeit, mit der die zukünftigen Wertveränderungen die Höhe des EaR voraussichtlich nicht überschreiten oder unterschreiten (bei Betrachtung der Verluste) wird.¹²⁸ In der Praxis stützt sich die Quantifizierung des ökonomischen Kapitals auf ein Sicherheits- bzw. Konfidenzniveau von mindestens 99% über einen Ein-Jahres-Horizont. Ein Konfidenzniveau von 99% bedeutet, dass der Wert der Zufallsvariable mit einer Wahrscheinlichkeit von nur 1% außerhalb des zu dieser Konfidenz gehörenden Intervalls liegt. Hinsichtlich der Betrachtung des Downside-Risikos wird ein einseitiges Konfidenzintervall betrachtet.

Das Konfidenzniveau kann z.B. aus dem jeweils angestrebten externen Unternehmensrating ableitet werden. So rechnet die HypoVereinsbank AG mit einem Konfidenzniveau von 99,97%.¹²⁹ Das Risiko, dass mit einer Wahrscheinlichkeit von 0,03% der Wert der Zufallsvariable außerhalb des entsprechendem Intervalls liegt, korrespondiert i.d.R. mit dem Zielrating der Bank, welches die Ausfallwahrscheinlichkeit für das Unternehmen in seiner Gesamtheit ausdrückt.

Abbildung 6: Graphische Darstellung des VaR-Ansatzes für Geschäftsrisiken

Die Risikoperiode bzw. Haltedauer hat ebenfalls einen wichtigen Einfluss auf die EaR. „Die Risikoperiode gibt die Länge der Periode an, für die die EaR als Risikopotenzial zu berechnen sind. Hierbei geht man von der Annahme aus, dass die betrachtete Position während dieses Zeitraums unverändert bleibt. Unter dieser Voraussetzung bringt eine längere Risikoperiode i.d.R. höhere EaR mit sich, da eine größere Wert-änderung in einem längeren Zeitintervall als wahrscheinlicher angesehen wird.“¹³⁰

In der Fortsetzung der zuvor hergeleiteten Standardabweichung kann diese bei der Normalverteilungsannahme über die Wurzel-T-Regel auf die jeweilige Risikoperiode bzw. Haltedauer normiert. So kann z.B. eine quartalsweise ermittelte Standardabweichung der Erträge durch die Multiplikation mit der √4 auf die Jahresbetrachtung hin angepasst werden.

Abschließend soll an dieser Stelle die Datenbasis und Datenherkunft diskutiert werden. Hier stellt sich die Frage, ob bei der Herleitung der Standardabweichung historische, zukunftsbezogene oder auf historischen Daten aufbauende Zukunftsmodellannahmen berücksichtigt werden sollen.

Generell baut das EaR-Konzept auf historischen Datenbeständen auf. Dabei ist eine Entscheidung hinsichtlich der zu berücksichtigenden Historienlänge zu treffen. Wird eine sehr lange Datenhistorie für einen Risikoparameter festgelegt, kann u.U. ein eher stabiler Verlauf in den Vorjahren stärkere Schwankungen in der jüngsten Vergangenheit so stark reduzieren, dass die EaR unterbewertet bleibt. Im umgekehrten Fall kann eine sehr kurz festgelegte Betrachtungsperiode mit hohen Schwankungen eine Überbewertung des EaR nach sich ziehen. Damit muss der Datenauswahl eine besondere Aufmerksamkeit gewidmet werden, die z.B. im Rahmen einer Expertenrunde diskutiert und entschieden werden könnte.

In der Zusammenführung der zuvor dargestellten Einflussgrößen auf das EaR-Konzept kann für die beiden Risikoparameter das jeweilige EaR wie folgt ermittelt werden.

Ein Vorteil dieses Konzeptes begründet sich in der Situation, dass sich die für die jeweiligen Risikoparameter ermittelten VaR/EaR-Werte aufgrund der gemeinsamen Basis zu einem Gesamtportfoliorisiko zusammenfassen lassen. Dabei können jedoch die einzelnen EaR-Werte nicht einfach aufsummiert werden. Es müssen vielmehr die zwischen den Risikoparametern bestehenden Risikoverbundeffekte bzw. Diversifikationseffekte berücksichtigt werden. Eine Aussage über die mögliche Risikoverbundeigenschaft bzw. Diversifikationswirkung zwischen zwei Positionen liefert der Korrelationskoeffizient =ρ¹³¹ . Die nachfolgende Formel beschreibt diesen Zusammenhang.

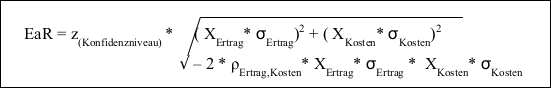
Die EaR-Größe kann mittels eines Skalierungsfaktors in eine Marktwertschwankung und damit auf den VaR überführt werden. Damit wird die Auswirkung eines nachhaltigen Ergebniseinbruches auf den Unternehmenswert berücksichtigt wird. Der Skalierungsfaktor kann beispielsweise den durchschnittlichen Steuersatz (x), die Eigenkapitalkosten (Cost of Equity = CoE) und den zeitlichen Betrachtungshorizont (t) berücksichtigen.

Für den Value at Risk (EaR) ergibt sich folgende formelmäßige Zusammenfassung:

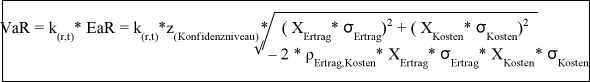
Da in dem vorgestellten Konzept Standardszenarien/Normalverteilungen für die Risiken betrachtet werden, bleiben in der Folge außergewöhnliche und sehr unwahrscheinliche Schwankungen der Risikoparameter häufig unberücksichtigt.

Das bewertete Risikoergebnis kann so fehlerhaft, d.h. zu hoch oder zu niedrig bewertet, sein.

Diese Problematik veranlasste die BaFin im Rahmen der MaRisk die Durchführung „regelmäßiger und angemessener Stresstests für die wesentlichen Risiken“ einzufordern. Dabei sollen die Stresstests „auch außergewöhnliche, aber plausibel mögliche Ergebnisse abzubilden“, die auf „geeigneten historischen und hypothetischen Szenarien“ basieren.¹³²

Neben dem Varianz-Kovarianz-Ansatz, bei dem die Wertveränderungen der Risikoparameter statistisch mithilfe der Normalverteilung modelliert werden, bieten zwei weitere Methoden einen ergänzenden Überprüfungsansatz für eine alternative Bestimmung der Verteilung der Risikoparameterveränderungen im Rahmen von Simulationsrechnungen.

Die historische Simulation löst sich von der Normalverteilung und verzichtet auf eine analytische Untersuchung der Risikofaktoren. Stattdessen werden die Wertveränderungen aus einer bestimmten Datenhistorie für die Schätzungen der zukünftigen Veränderungen übernommen. Dabei wird überprüft, welche Ergebnisabweichungen zu erwarten sind, wenn sich die in der Vergangenheit beobachteten Veränderungen nochmals wiederholen. Auch hier besteht die Herausforderung der richtigen Auswahl des optimalen Zeitfensters in der Vergangenheit. Zu alte Daten können irrelevant geworden sein, zu kurze Zeitfenster lassen die Repräsentativität der Auswahl fraglich erscheinen.

Neben der Notwendigkeit eines großen Datenhaushaltes besteht auch hier die Unsicherheit in der Zukunftsbeurteilung. Was es in der Vergangenheit nicht gab, wird es in diesem Modell auch in Zukunft nicht geben.

Bei der Monte Carlo Simulation können auf der Basis von Zufallszahlen beliebige Erwartungswerte und Standardabweichungen für die Zukunft unterstellt und beliebige Verteilungen zugrunde gelegt werden. Statt der Verwendung von historischen Wertänderungen wird die Unsicherheit über das zukünftige Verhalten der Risikofaktoren mit Zufallszahlen angegangen. Dieses Modell wird vorwiegend für komplexe Risikostrukturen eingesetzt.

Für die „einfachen“ Risikostrukturen, bei denen ein linearer Zusammenhang zwischen Veränderungen der Risikofaktoren und Wertänderungen der Ergebnisgrößen besteht, ist ein Normalverteilungsansatz ebenso ausreichend wie eine historische Simulation.

¹²⁴ „Ein p-Quantil ist ein Lagemaß in der Statistik, wobei p eine reelle Zahl zwischen 0 und 1 ist. Das p-Quantil ist ein Merkmalswert, der die Verteilung einer Variablen bzw. Zufallsvariablen in zwei Teile teilt. Links vom p-Quantil liegen 100 * p Prozent aller Beobachtungswerte bzw. 100 * p Prozent der Masse der Zufallsvariablen. Rechts davon liegen 100 * (1-p) Prozent aller Beobachtungswerte bzw. 100* (1-p) Prozent der Masse der Zufallsvariablen.“ http://de.wikipedia.org/wiki/Quantil (19.01.2010).
¹²⁵ Vgl. Schierenbeck/Lister (2002) S. 339.
¹²⁶ Vgl. Schierenbeck/Lister (2002) S. 339.
¹²⁷ Vgl. Koch, U. (2005), S. 14f.
¹²⁸ Vgl. Auer, M. (2002), S. 14f.
¹²⁹ HypoVereinsbank AG (Geschäftsbericht 2008), S. 46.
¹³⁰ Koch, U. (2005), S.17.
¹³¹ Der Korrelationskoeffizient stellt ein statistisches Maß für die Stärke des Zusammenhangs der Entwicklung zweier Zufallsvariablen dar. Bei einem Korrelationskoeffizienten von +1 verläuft die Entwicklung zweier Beobachtungsgrößen vollständig gleichgerichtet, bei einem von -1 entgegengesetzt und bei einem von 0 ist keinerlei Zusammenhang zu erkennen.
¹³² BaFin (MaRisk, AT 4.3.2 Risikosteuerung- und -controllingprozesse, Ziffern 3 und 4).